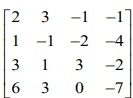22MATS11 Set β 1 Solved Model Question Paper 1st semester P cycle for Computer Science and Engineering (CSE) Stream 22 Scheme
MODULE β 1
1.A] With usual notation prove that \tan\phi=r\frac{d \theta}{dx}
2.B] Find the angle between the curves π = πππππ and r=a/logπ
1.C] x=a(\theta+\sin\theta), y=a(1-cos\theta) is 4acos(\frac{\theta}{2}) Show that the radius of curvature at any point π on the cycloid
OR
2.A] Show that the curves π = π(1 + π πππ) and π = π(1 β π πππ) cuts each other orthogonally
2.B] Find the pedal equation of the curve \frac{2a}{r}=(1+cos\theta)
2.C] Find the radius of curvature for the y^{2}=\frac{4a^{2}\left( 2a-x \right)}{x} curve, where the curve meets the x-axis.
MODULE β 2
3.A] Expand log(π πππ₯) up to the term containing π₯ 4 using Maclaurinβs series.
3.B] If π’ = π ππ₯+ππ¦π(ππ₯ β ππ¦) prove that π (ππ’/ππ₯) + π (ππ’/ππ¦) = 2πππ’ by using the concept of composite functions.
3.C] Find the extreme values of the function π(π₯, π¦) = π₯ 3 + 3π₯π¦ 2 β 3π¦ 2 β 3π₯ 2 + 4
OR
4.A] Evaluate i) \lim_{x \to 0} \left( \frac{a^{x}}{b^{x}} \right)^{\frac{1}{x}}. ii) \lim_{x \to 0} \left( \frac{tanx}{x} \right)^{\frac{1}{x}}
4.B] If π’ = π(π₯ β π¦, π¦ β π§, π§ β π₯) show that ππ’/ππ₯ + ππ’/ππ¦ +ππ’/ππ§ = 0
4.C] If π₯ + π¦ + π§ = π’, π¦ + π§ = π£ πππ π§ = π’π£π€, find the values of π(π₯,π¦,π§)/π(π’,π£,π€).
MODULE β 3
5.A] Solve ππ¦/ππ₯ + π¦/π₯= π₯2π¦6
5.B] Find the orthogonal trajectories of π₯2 /π2 +π¦2/π2+π= 1, where Ξ» is a parameter.
5.C] Solve π₯π¦π2β(π₯2 + π¦2)π+π₯π¦ = 0
OR
6.A] Solve (π₯2 + π¦2 + π₯)ππ₯ + π₯π¦ππ¦ = 0
6.B] When a switch is closed in a circuit containing a battery E, a resistance R and an inductance L, the current i build up at a rate given by L di dt Ri = E. Find i as a function of t. How long will it be, before the current has reached one-half its final value, if E = 6 volts, R = 100 ohms and L = 0.1 henry?
6.C] Find the general solution of the equation (ππ₯ β π¦)(ππ¦ + π₯) = π2π by reducing into Clairautβs form by taking the substitution π = π₯2, π = π¦2
MODULE β 4
7.a] Find the least positive values of x such that
i) 71 β‘ π₯(πππ8)
ii) 78 + π₯ β‘ 3(πππ5)
iii) 89 β‘ (π₯ + 3)(πππ4)
7.B] Find the remainder when (349 Γ 74 Γ 36) is divided by 3
7.C] Solve 2π₯ + 6π¦ β‘ 1(πππ7)
4π₯ + 3π¦ β‘ 2(πππ7)
OR
8.A] i) Find the last digit of 72013
ii) Find the last digit of 1337
8.B] Find the remainder when the number 21000 is divided by 13
8.C] Find the remainder when 14! is divided by 17
MODULE β 5
9.A] Find the rank of the matrix
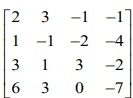
9.B] Solve the system of equations by Gauss-Jordan method x+y+z+=10, 2x-y+3z=19, x+2y+3z=22.
9.C] Using power method find the largest eigenvalue and the corresponding eigenvector of the matrix A =
OR
10.A] Solve the following system of equations by Gauss β Seidel method 10x+y+z=12, x+10y+z=12, x+y+10z=12.
10.B] For what values of a and b the system of equation x + y + z = 6: x + 2y + 3z = 10: x + 2y + az = b has i) no solution
ii) a unique solution and
iii) infinite number of solution
10.C] Solve the system of equations by Gauss elimination method
x + y + z = 9, x β 2y + 3z = 8, 2x + y β z = 3
.
